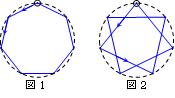円周上に等(とう)間隔(かんかく)に7つの点をとり, そのうち1つの点を選びます。

この点から時計と反対まわりに, “指定された個数”だけ飛(と)ばしたところにある点を次々(つぎつぎ)に選び, これらの点を直線で順番に, 一筆(ひとふで)書(が)きで結んでいきます。

この一筆書きを, 最初の点に戻(もど)ってくるまで続けます。

例えば, “指定された個数”が0個のときは, 1つの点を飛ばさないので, 図1のよう

な正七角形ができます。

この図を7☆0と表すことにします。また,“指定された個数”が1個のときは図2のような図ができ, これを7☆1と表すことにします。

このように, ☆の右側には, 飛ばす点の個数0, 1, 2,3, 4, 5のいずれかが入ることになります。

このとき, 次の各問いに答えなさい。【早稲田大学高等学院中学部】

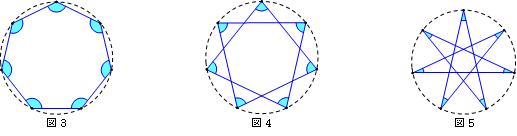
(1) 次の図3は, 図1の角に印(しるし)をつけたものです。印をつけた角をすべてたすと何度になるか求めなさい。

(2) 次の図4は, 図2の角に印をつけたものです。印をつけた角をすべてたすと何度になるか求めなさい。

(3) 次の文の□にあてはまる数について, 次の①, ②の問いに答えなさい。次の図5は7☆□の図です。

　　① □にあてはまる数は何通りあるか求めなさい。　　　② □にあてはまる数をすべて求めなさい。

(4) 次の図5で印をつけた角をすべてたすと何度になるか求めなさい。

解法

(1) 公式㉑により, 180×(7－2)＝900°

　　◎「多角形の内角の和」の公式◎

　　　　　180×(□－２)

(2) 裏技により, 180×(7－4)＝540°

　　◎星形多角形(1つ飛ばし)の内角の和を求める裏技◎ 

　　　　　180°×(□－４)

(3) 下の図のように, PからQまで左周りなら2個飛ばし, 右回りなら3個飛ばしなので2通りで,7☆2または, 7☆3となります。

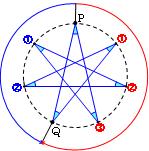
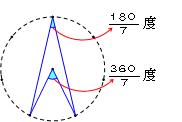
(4) 下の図のように, 1ヶ所の中心角が （３６０÷７）度なので,円周角は （１８０÷７）度だから, 

　　 （１８０÷７）度×7＝180°となります。

解答　(1)900° (2) 540° (3) 2通り, (7☆)2または, (7☆)3  (4)180°

9月1日に, 私の著書, 私立国立中学入試対策『算数の極意』がついに出版となりました!!

22年前, とある塾で文系の私はなぜか算数・数学の授業を命ぜられ,とても苦労しました。

そんな時に, 「こんな本があったらな～」という思いで,ずっと書きためたものです。

全国の書店の他, AMAZON, 楽天市場でも購入できます。【宣伝!!(^^)!!】